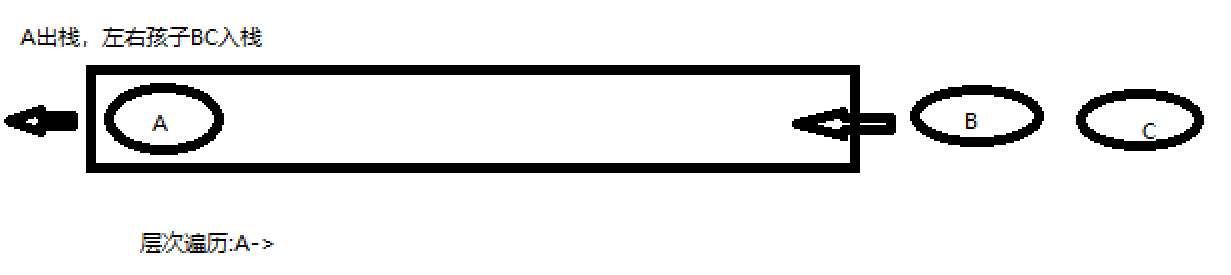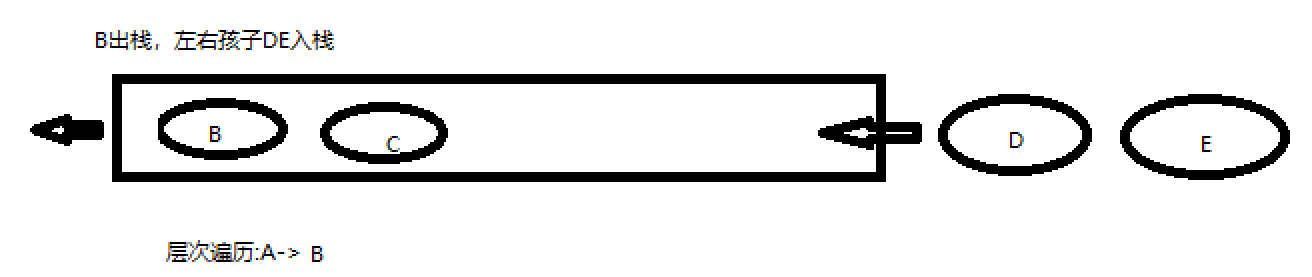二叉树的概念

每个节点至多有两个孩子的树叫做二叉树

二叉树的存储结构

1
2
3
4
5
typedef struct bTree{
	char ele;
	struct bTree* lchild;
	struct bTree* rchild;
}bTree;

二叉树节点使用结构体存储，包含数据域和指针域。指针域为分别指向左右孩子的指针

二叉树的创建

二叉树的创建方式有很多种，在这里我们根据树的先序遍历序列来创建一个二叉树

创建根节点

1
struct bTree* root=(struct bTree*)malloc(sizeof(struct bTree));

树的先序序列如下，其中##代表空节点

1
2
char *data="ABD##E##CF##G##";
int index=0;

树的结构为

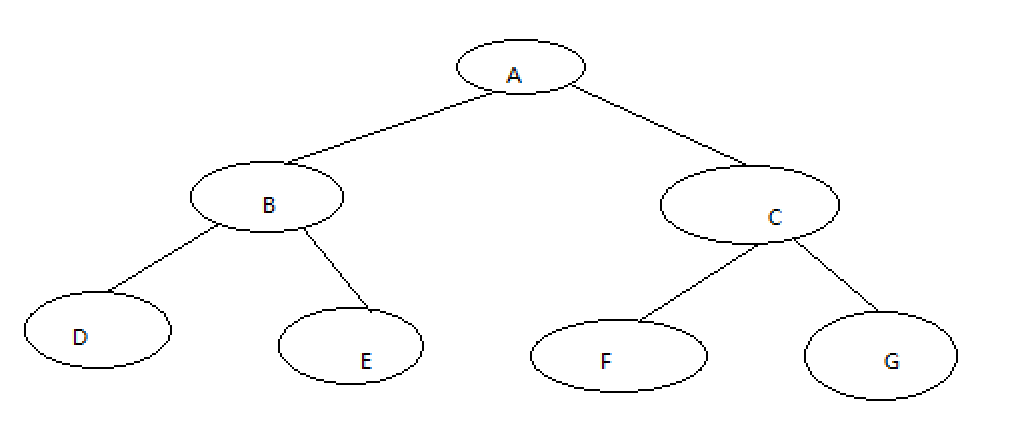
image-20240116152254240

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void create_tree(bTree **root,char *data,int *index){
	char ch;
	ch=data[*index];
	(*index)++;	
	/*空节点返回*/
	if(ch=='#'){
		(*root)=NULL;
		return;
	}
	/*结点有数据*/
	(*root)=(struct bTree *)malloc(sizeof(bTree));
	(*root)->ele=ch;
	create_tree(&(*root)->lchild,data,index);
	create_tree(&(*root)->rchild,data,index);

}

二叉树的遍历

二叉树的遍历主要包括：前序遍历，中序遍历，后序遍历和层次遍历。

前序遍历

前序遍历的顺序为:root->lchild->rchild 。先序是对于根节点而言的。对于每一个节点，先访问根节点root，再先序遍历以root的左孩子为根节点的子树，最后先序访问root的右孩子为根节点的子树。

下面是树的先序遍历过程：

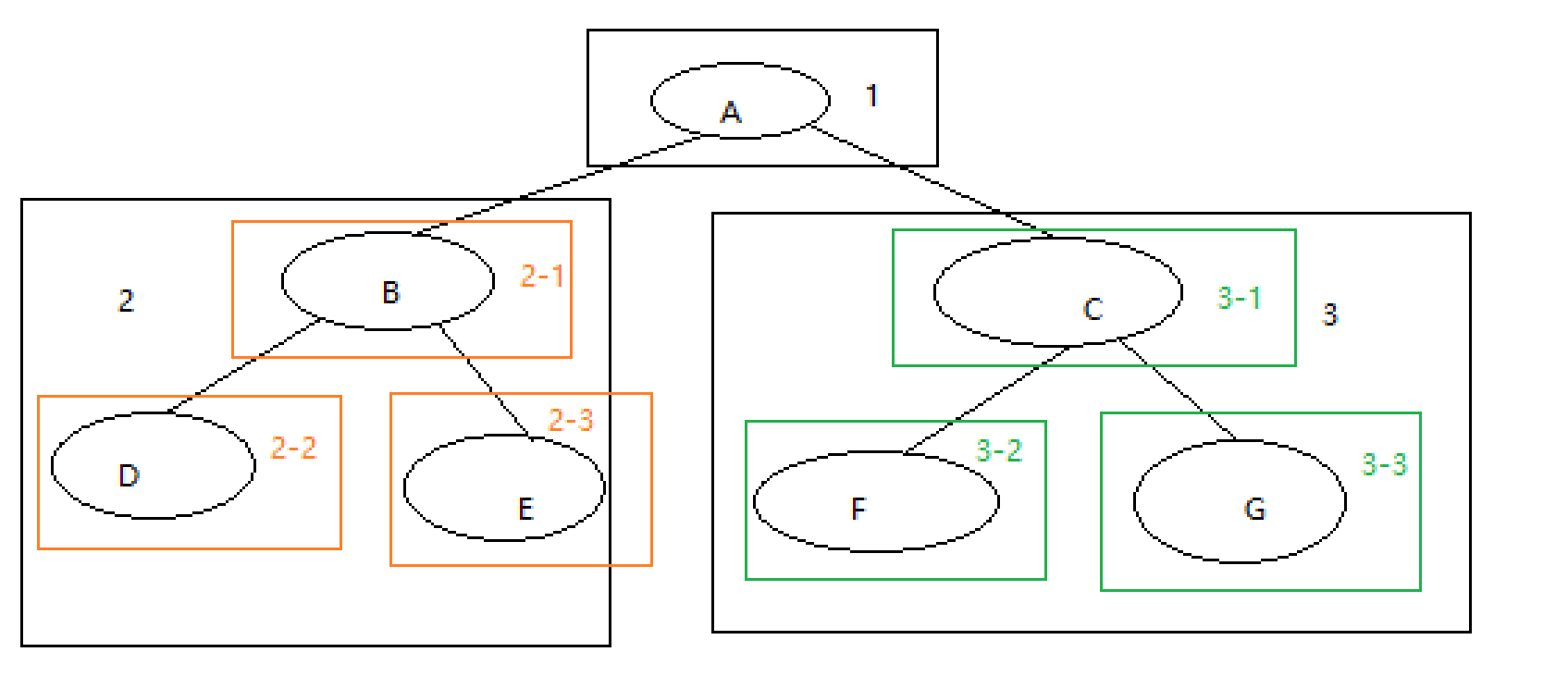
对于根节点A，我们的访问顺序为：先访问A，后访问A的左部分，最后访问A的右部分。

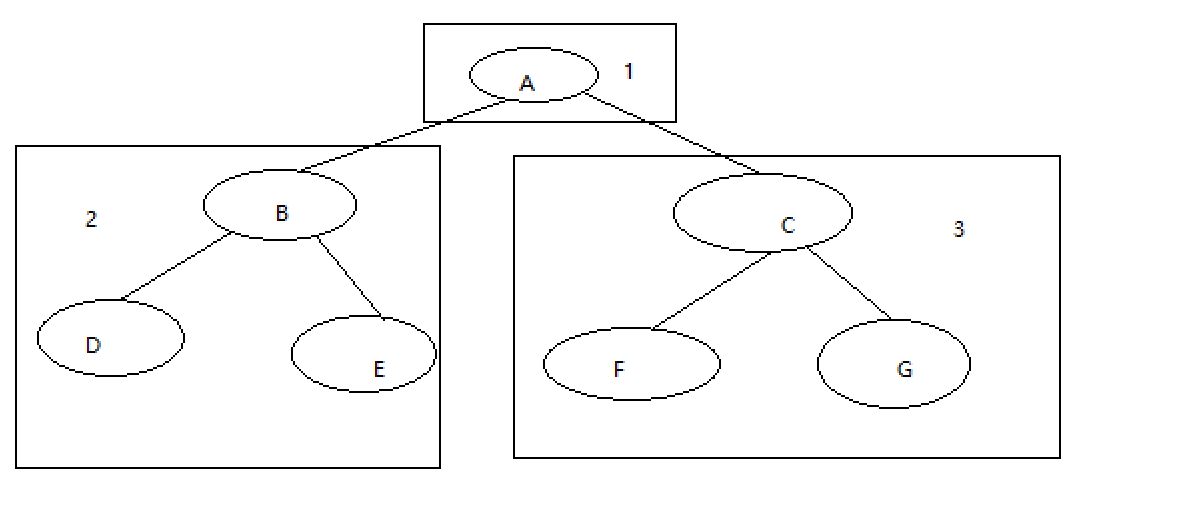
image-20240116152854286

首先我们访问A节点，遍历序列:A->

之后我们访问A的左部分，即部分2。对于部分2，仍是采用先根节点，后左节点，最后右节点的顺序进行。于是遍历顺序:A->B->D->E

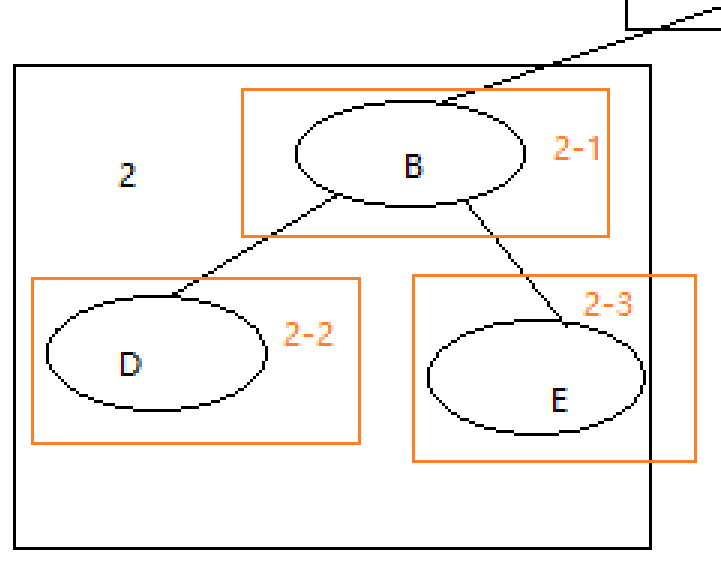
image-20240116153334178

最后我们访问A的右部分，先根后左，最后为右节点.得到遍历顺序：A->B->D->E->C->F->G

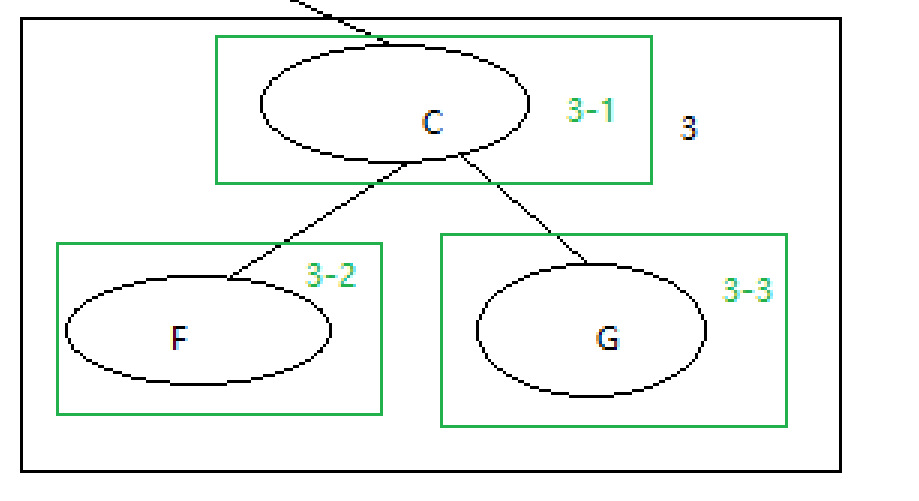
image-20240116153829290

image-20240116153915848

代码部分如下

1
2
3
4
5
6
7
8
9
10
11
void preoder_traversal(struct bTree* root){
	if(root==NULL){
		return;
	}
	else{
		printf("%c->",root->ele);
		preoder_traversal(root->lchild);
		preoder_traversal(root->rchild);
	}

}

代码中，我们首先判断要访问的节点是否为空，为空则函数返回，不进行节点访问。若不为空，则先打印节点数据，然后递归访问左子树，在递归访问右字数

中序遍历

中序遍历和先序遍历原理相似，其遍历顺序为：先访问左子树，后访问根节点，最后访问右子树

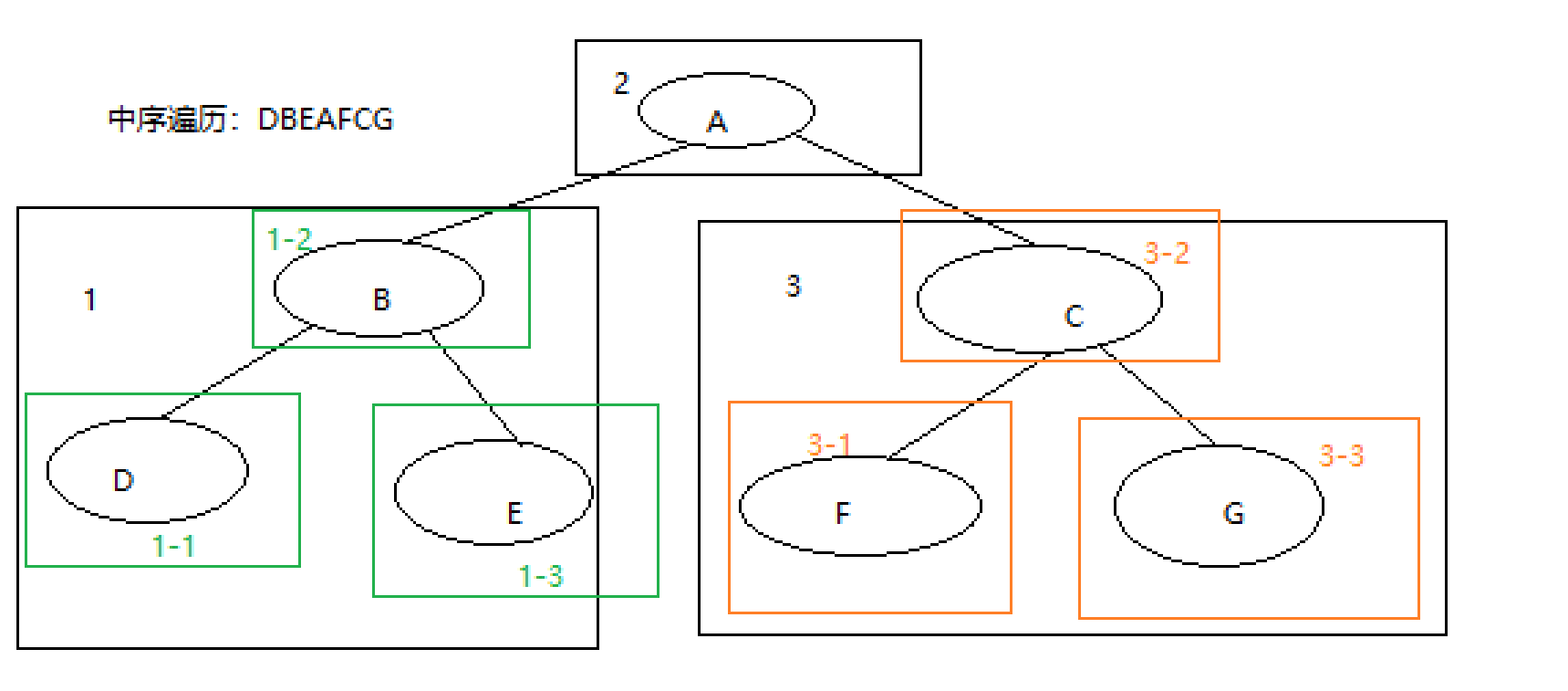
image-20240116154703168

中序遍历代码

1
2
3
4
5
6
7
8
9
10
11
12
void inoder_traversal(struct bTree* root){
	if(root==NULL){
		return;
	}
	else{
		
		inoder_traversal(root->lchild);
		printf("%c->",root->ele);
		inoder_traversal(root->rchild);
	}

}

后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
void postoder_traversal(struct bTree* root){
	if(root==NULL){
		return;
	}
	else{
		
		postoder_traversal(root->lchild);
		postoder_traversal(root->rchild);
		printf("%c->",root->ele);
	}

}

层次遍历

二叉树的层次遍历为从根子树所在层开始，按层从左往右遍历。

image-20240116152254240

上面这颗树的层次遍历顺序为:A->B->C->D->E->F->G。层次遍历可以通过队列实现。

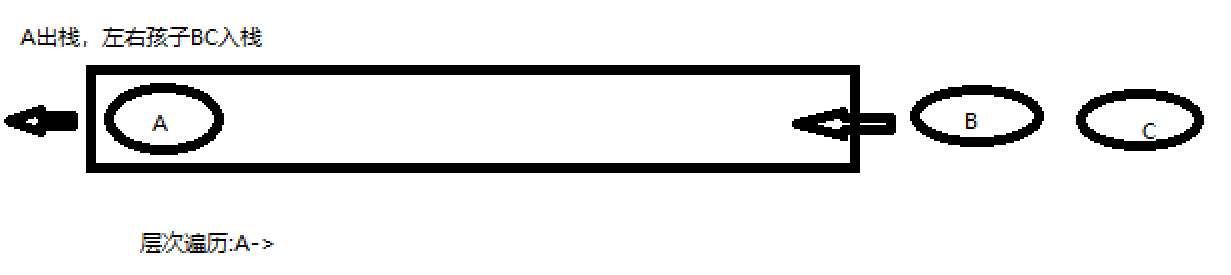
image-20240228211735228

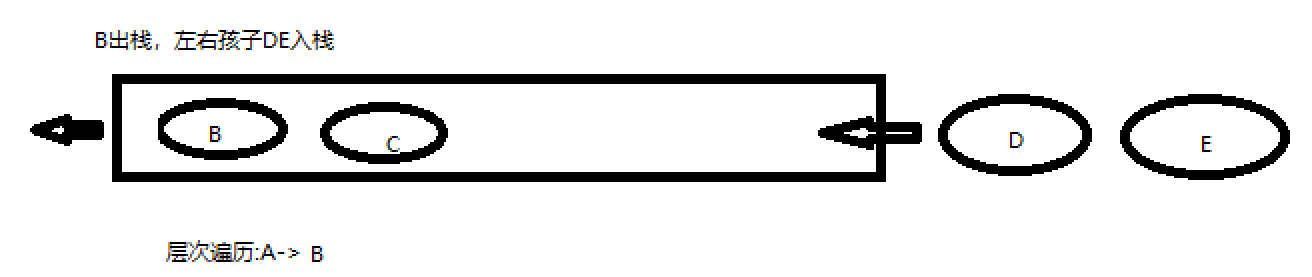
image-20240228212012585

代码实现:

队列结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
typedef struct QueueNode{
	struct bTree* treenode;
	struct QueueNode *pre;
	struct QueueNode *next;
}QueueNode;

struct QueueNode* init_queue(){

	struct QueueNode *head=(struct QueueNode*)malloc(sizeof(struct QueueNode));
	head->treenode=NULL;
	head->next=head;
	head->pre=head;
	return head;
}

void en_queue(struct bTree* treenode,struct QueueNode *head){
	struct QueueNode *node=(struct QueueNode*)malloc(sizeof(struct QueueNode));
	node->treenode=treenode;
	
	node->next=head;
	node->pre=head->pre;

	head->pre->next=node;
	head->pre=node;
}

struct QueueNode* de_queue(struct QueueNode* head){
	/*队列为空*/
	if(head->next==head){
		return NULL;
	}
	else{
		struct QueueNode* tmp=head->next;
		head->next=head->next->next;
		head->next->pre=head;
		return tmp;
	}

}

层次遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void layer_travesal(struct QueueNode* head){

	/*队列为空*/
	if(head->next==head){
		return;
	}
	struct QueueNode* node=de_queue(head);
	struct bTree* treenode=node->treenode;	
	printf("%c->",treenode->ele);
	if(treenode->lchild!=NULL){
		en_queue(treenode->lchild,head);
	}	
	if(treenode->rchild!=NULL){
		en_queue(treenode->rchild,head);
	}
	layer_travesal(head);
	
}