算法介绍

普利姆算法是一种图算法，用于构建最小生成树。最小生成树的顶点全部连通，即沿任意顶点出发，可以达到图的全部顶点，且其所有边的权值最小。

算法描述:

从最小生成树集合中选择边权值最小且不在生成树集合中的顶点加入最小生成树集合，重复上述操作直到全部的点加入最小生成树集合。

算法实现

现有5个村落(编号为0-4)需要在各个村庄中修路，使各村庄联通，且代价最小。

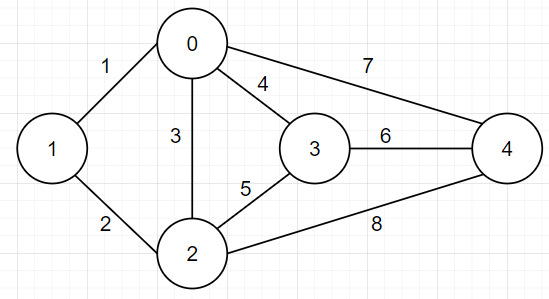
image-20240324211139894

这里我们使用邻接矩阵来表示上图

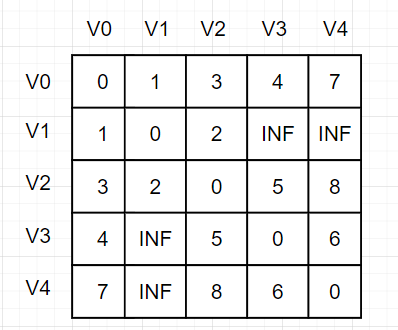
image-20240324211232193

普利姆算法执行过程

实现普利姆算法需要利用两个辅助数组lowcost和edge。

lowcost数组用于保存最小生成树集合到各顶点的距离，数组索引与顶点相关联。l例如owcost[3]表示最小生成树集合到顶点4的距离

如果数组中元素值为0则表示顶点存在于最小生成树集合，否则表示权值大小。

edge用于存储顶点的边关系，edge[1]=2表示与节点1与节点2相连。

1
2
int lowcost[graph->vexnum];
int edge[graph->vexnum];

执行过程：

  1. 选定一个节点加入最小生成树集合,初始化lowcost和edge数组

  2. 重复下面3的步骤，直到所有的顶点都加入最小生成树集合

  3. 选择lowcost数组中权值最小的顶点，加入最小生成树集合,利用新加入的顶点更新lowcost数组和edge数组

代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
 int lowcost[graph->vexnum];
 int edge[graph->vexnum];
/*选择起点，利用lowcaast更新lowcoast*/
    for(int i=0;i<graph->vexnum;i++){
        lowcost[i]=graph->matrix[0][i];
        edge[i]=start;
    }
lowcost[start]=0;//0表示加入生成树集合
for(int i=1;i<graph->vexnum;i++){//
        int min=1024;//最小权值
        int minindex=-1;
        //选择最小权值,且没有加入最小生成树
        for(int j=0;j<graph->vexnum;j++){
            if(lowcost[j]<min&&lowcost[j]!=0){//
                min=lowcost[j];
                minindex=j;
            }     
        }
        //最小权值的顶点标记为已经加入生成树集合
       lowcost[minindex]=0;
        printf("边(%d,%d)的权值为%d\n",edge[minindex],minindex,min);
        //更新lowcoast
        for(int j=0;j<graph->vexnum;j++)
            if(lowcost[j]>graph->matrix[minindex][j]){
                lowcost[j]=graph->matrix[minindex][j];
                edge[j]=minindex;//j由最小权值顶点构建(j,minindex)
        }
    }
}

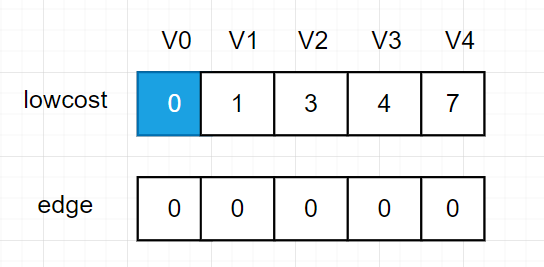
这里我们选择顶点0加入最小生成树结合，

lowcost数组值为最小生成树集合到各顶点的距离，由于集合中只有顶点V0，所以lowcost[0]被设置为了0，其余值为设置为顶点0到其余点的距离。edge数组被初始化为0，表示顶点0与其他边相连。

image-20240324211839053

1
2
3
4
5
6
7
8
int lowcost[graph->vexnum];
int edge[graph->vexnum];
/*选择起点，利用lowcaast更新lowcoast*/
    for(int i=0;i<graph->vexnum;i++){
        lowcost[i]=graph->matrix[0][i];
        edge[i]=start;
    }
lowcost[start]=0;//0表示加入生成树集合

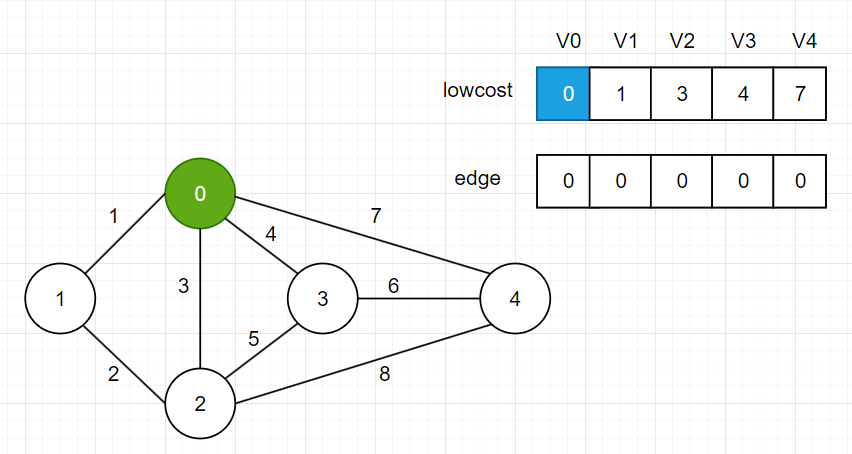
image-20240324214402057

之后遍历lowcost数组找到最小权值1和对应顶点V1，选择V1加入最小生成树集合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
for(int i=1;i<graph->vexnum;i++){//
      int min=1024;//最小权值
      int minindex=-1;
      //选择最小权值,且没有加入最小生成树
      for(int j=0;j<graph->vexnum;j++){
          if(lowcost[j]<min&&lowcost[j]!=0){//
              min=lowcost[j];
              minindex=j;
          }     
      }
      //最小权值的顶点标记为已经加入生成树集合
     lowcost[minindex]=0;
     /*.....*/
}

V1加入集合后，遍历与V1相邻的边，如果边的权值<对应owcost的权值，则更新lowcost和edge

1
2
3
4
5
for(int j=0;j<graph->vexnum;j++)
            if(lowcost[j]>graph->matrix[minindex][j]){
                lowcost[j]=graph->matrix[minindex][j];
                edge[j]=minindex;//j由最小权值顶点构建(j,minindex)
 }

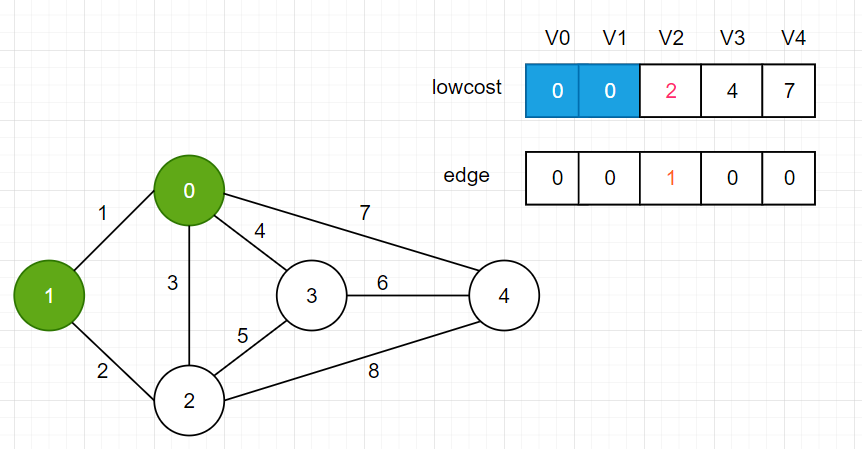
image-20240324214813150

重复上面的步骤，选择顶点2加入最小生成树集合，V2邻边距离均大于lowcost数组值，lowcost数组不更新

image-20240324215725109

选择V3加入最小生成树集合，更新lowcost[4]的值，以及egde[4]的值

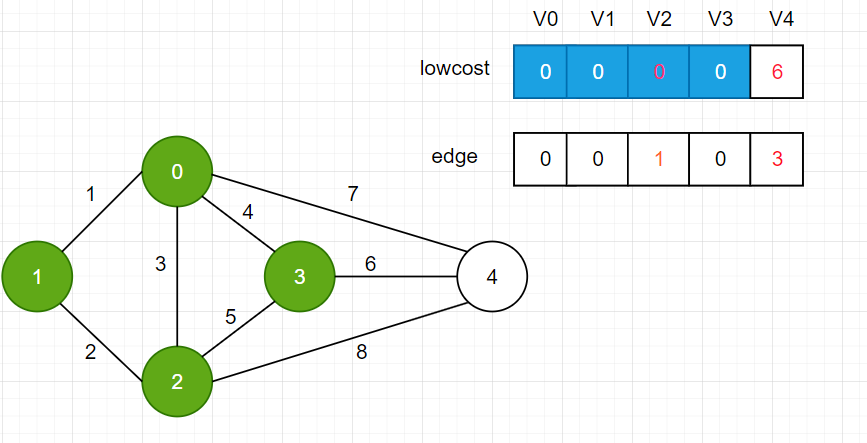
image-20240324215832341

选择V4加入集合

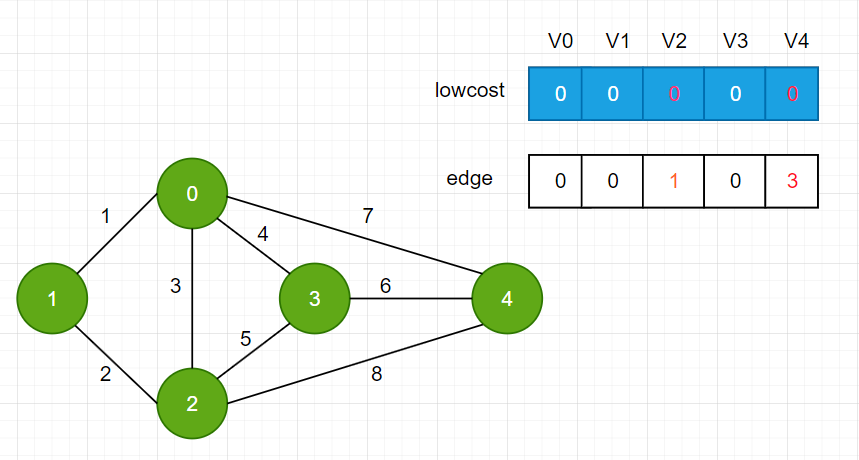
image-20240324215918888

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
void Prim(Graph *graph,int start){

    int lowcost[graph->vexnum];
    int edge[graph->vexnum];
   

   /*选择起点，利用lowcaast更新lowcoast*/
    for(int i=0;i<graph->vexnum;i++){
        lowcost[i]=graph->matrix[0][i];
        edge[i]=start;
    }

    lowcost[start]=0;//0表示加入生成树集合

    for(int i=1;i<graph->vexnum;i++){//
        int min=1024;//最小权值
        int minindex=-1;
        //选择最小权值,且没有加入最小生成树
        for(int j=0;j<graph->vexnum;j++){
            if(lowcost[j]<min&&lowcost[j]!=0){//
                min=lowcost[j];
                minindex=j;
            }     
        }
        //最小权值的顶点标记为已经加入生成树集合
       lowcost[minindex]=0;
       
      
        printf("边(%d,%d)的权值为%d\n",edge[minindex],minindex,min);
        //更新lowcoast
        for(int j=0;j<graph->vexnum;j++)
            if(lowcost[j]>graph->matrix[minindex][j]){
                lowcost[j]=graph->matrix[minindex][j];
                edge[j]=minindex;//j由最小权值顶点构建(j,minindex)
        }
    }
}

运行结果

image-20240324215352752